1/logx 積分 288320-1/logx 積分
No1 ベストアンサー 回答者: springside; · 微分しても、新しい関数は出来ません。 ところが、積分することで、いくらでも、新しい関数を定義することが可能です。 ∫ (1/logx)dx,∫ (e^x/x)dx,∫ (sinx/x)dx,∫ (cosx/x)dx,・問113 次の広義積分が収束するかどうか判定せよ (1) ∫ 1 0 e x sin(x2)dx, (2) ∫ 1 0 logx 1 x dx 解答例 (1) je x sin(x2)j e x (x 0) で, 広義積分 ∫1 0 e x dxが収束するので, 比較判定法より, 広義積分 ∫ 1 0 e x sin(x2)dx も収束する (2) f(x) = logx 1 x は0 < x < 1で連続であるが

Y Logx Dy Dx
1/logx 積分
1/logx 積分-B1です, 積分と級数が好きです 少し簡単めの, 大学受験向けの記事を書くかもしれません 関連記事 ∫0,1 (x^2 1)/logx dxの計算 ディガンマ関数の基本性質と積分表示 フーリエ変換しても変わらない関数 コメント コメントはありません。 Mathlog 数学特化の情報共有サービス 使い方 利用 · 対数微分法を用いた例題 次の関数を微分せよ。 〈解答〉 パッと見た感じ、logを使うようには見えないんだけど 今回の関数を微分するためには対数微分法というやり方を用います。 まずは、底 とする対数を両辺にとります。 ここから両辺を微分すると



干货 送你一套数学微积分常用公式大全
Yet another direct way forward is to use Frullani's Integral To that end, let I(a) be the integral given by I(a) = ∫1 0xa − 1 logx dx Enforcing the substitution logx → − x yields I(a) = ∫∞ 0 e − ax − 1 x e − xdx = − ∫∞ 0 e − ( a 1) x − e − x x dx whereupon using Frullani's Integral we obtain(C1) 1 In = ∫ sinn xdx とする(不定積分).部分積分の公式でf = sinn 1 x;g = cosx と すると In = sinn 1 xcosx (n 1) ∫ sinn 2 xcos2 xdx = sinn 1 xcosx (n 1)(I n 2 In) よってIn = 1 n sin n 1 xcosxn 1 n In 2 をえる.ゆえにJn = 1 n sin n 1 xcosxˇ=2 0 n 1 n Jn 2 である. 2 J0 J1 は明らかなので,(1) とあわせると 1 J2n J2n1 J2n 1 J2n1 · 積分 ∫ dx 1 x2 を計算しよう。 *1 方針: x = tanθ とおき、置換 積分 をする。 *2 ここで tan − 1 は tan の 逆関数 *3 。 逆 三角関数 の記号は高校の教程には出てこない。 でも逆 三角関数 を解く問題、例えば tanθ = √3 θ = π 3 nπ という計算は解かせ
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! · 1/x (logx1) をxで積分してください。Integral of 1/ (x log x) \square!
1 積分練習問題解答 1 つぎの不定積分を計算せよ。 (1) ∫ x 1 x2 2x5 dx d dx (x2 2x5) = 2(x1)だから x 1 x2 2x5 x1 x2 2x5 2 x2 2x5 と変形して,y = x2 2x5 とおくとdy = 2(x1)dx だから ∫ x1 x2 2x5 dx = ∫ dy 2y = logjyjC = 1 2 log(x2 2x5)C一方,後半の積分はx 22x5 = (x1) 4 なので,y = (x1)/2 と書くと · logx积分 1/x的积分为inx,那么inx的积分为多少呢,就是logX的积分为多少呢? 1/x的积分为 inx,那么inx的积分为多少呢, 就是 logX的积分为多少呢? 展开 分享 新浪微博 QQ空间 举报定期試験や入学試験などでは「解ける」問題だけが出題されていますが,各自で自由に思い浮かべた関数に対していつでもその不定積分を初等的に表現できるとは限らないことに注意してください. log x に関する不定積分≪一覧≫ ∫wn ( log x) n dx (n≠0) ∫wn log x dx=x log x−xC (*51) ∫wn ( log x) 2 dx=x ( log x) 2 −2x log x2xC (*52) I n = ∫wn ( log x) n dx (n=0,1,2




微博搜索



三道广义积分题 知乎
1/logxの微分の仕方を教えて下さい。 – (1/logx)'={( 合成関數の微分の問題ですy=log(x^2+1)の導関數を求めなさいやり {(logx)^2} – これをxについて微分してください 教えてくださいy=(logx)2乗を微分したときの答えと解き方を 查看其他搜尋結果 積分 logx /(x^2) を とおいて置換積分 · 1/log x の不定積分 1901 テーマ: 微分積分 ∫ 1/log x dx を考える t = log x と 置換積分 すると dx/dt積分する関数を入力してください 変数 被積分関数 log (1x) を次の変数で微分する x (x1)*log (x1)x1 注意 log 自然対数 グラフを描く LaTeXエディタで編集 このページへの直接のリンク 変数に次の値を代入する x= 積分電卓 解析積分を用いて所与の変数に対する関数の不定積分 (アンチ導出)を計算する。 また、関数のグラフとその積分を描画することもできる。




What Is The Integration Of 1 Log X Quora




Integral Of 1 X Ln X Substitution Youtube
積分 logx ∫ log x d x = ∫ 1 · log x d x と考えて部分積分を行なう. 部分積分の公式の ∫ f (x) g ′ (x) d x = f (x) g (x) − ∫ f ′ (x) g (x) d x において, f (x) = log x , g ′ (x) = 1 = x ′ として計算する. ∫ 1 · log x d x = ∫ x ′ · log x d x = x log x − ∫ x · (log x) ′ d x = x log x − ∫ x · 1 x d x = x log x − ∫ 1 · d x = x log x − x C = x (log x − 1) C考え方 log x の積分が求められない → 1· log x と考えて, log x を微分する側:現在 f の側とする. ( )は左辺の初めの形広義積分 例 定積分Z 1 0 1 √ x dx を考える。 これを次のように計算する のはそのままでは定義に反する: Z 1 0 1 √ x dx = 2 √ x 1 0 = 2 理由Z 1 0 1 √ x dx を定義する為のRiemann 和は発散し得
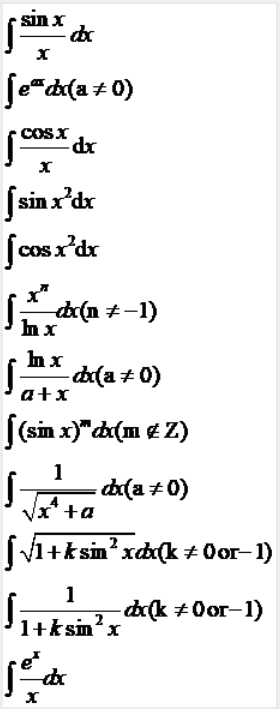



常见不可积积分 Thunderobot7的博客 Csdn博客 不可积函数




Sym Py Edu
· Integration of log x in pdf Integral of log x Hello students I am Bijoy and welcome to my educational forumToday we will deal with the Integration of logxThere we see various types of integration on logx, & also will see something about on the LIATE or ILATE rule of by parts method Integration of log x · \log x=1\cdot \log x logx = 1⋅logx とみなして部分積分を使います。Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



什么是黎曼和什么是定积分 信息阅读欣赏 信息村 K0w0m Com




Y Logx Dy Dx
数学 において、 対数積分 (たいすうせきぶん、 英 logarithmic integral function ) li (x) とは、全ての正の 実数 x ≠ 1 において次の 自然対数 ln を含む 定積分 によって定義される 特殊関数 である。微分積分学I 期末試験解答と講評 07 年9 月1 日 浪川 幸彦 問題1 次の関数を積分せよ(原始関数を求めよ)(積分定数は省略してよい): 1) 1 p x1 p x ;2) ex e x ex e x ;3)tanx ;4) 1 sinx ; 5)xn logx (n 2 Z) ;6) 1 x3 1 解 1) Z dx p x1 p x = Z (p x1 p x)dx = Z p x · 数Ⅲ定積分9(部分積分法。 logX=1・logXとしてlogXを微分するタイプ) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try




数学实验一元微积分基础实验1 函数与极限专题实验1 极限的应用基础实验2 微分及其应用专题实验2 选址问题 Ppt Download




如何用matlab求各种不定积分 搜狗指南
なって広義積分は存在しないことが分かるはずです。 問題922 教科書 例題510 次の広義積分が存在するかどうか判定し、存在 する場合はその値を求めて下さい(a > 0)。 (1) ∫ a 0 1 p a2 x2 dx (2) ∫ 1 0 e axdx (1) 0 < c < a とします。 ∫ c 0 1 p a2 x2 dx = ∫ c 0 1瞬間部分積分 1:三列の表をつくる。 二列目に上から 0 0 になる手前まで格納する。 \cdots ⋯ と格納する。 , , \cdots ,−,⋯ と交互に格納する。 4:横にかけて縦に足す。 \displaystyle\int x^2e^xdx ∫ x2exdx という不定積分は部分積分を二回行わないと解け · 数学 において、 コーシーの主値 ( 英 Cauchy principal value)とは、ある種の 広義積分 に対して定められる値のことである。 出典 フリー百科事典『ウィキペディア(Wikipedia)』 ただし、 a = b = ϵ > 0 とすると、 ∫ − ϵ − 1dx x ∫1 ϵdx x = logϵ (– logϵ) = 0 ∴ lim ϵ → 0(∫ − ϵ − 1dx x ∫1 ϵdx x) = 0 ∫1 0 dx √x(1 − x) = lim a → 0 0 b → 1 − 0∫b a dx √x(1 − x) t = √x




自然對數 维基百科 自由的百科全书



悟空问答 如何记住高等数学的积分表 21个回答
· 質問者: レモンサイダー 質問日時: 1615 回答数: 2 件 広義積分 ∫e→ ∞dx/ x (logx)^2 をもとめよ ただし広義積分の収束を仮定してよい 通報する この質問への回答は締め切られました。 質問の本文を隠す · 部分積分の仕方と迷わず計算する為のコツを紹介! <この記事の内容>:「積分法の基本公式(1)」に引き続き、今回は「部分積分の仕方」を紹介していきます。 タイトルの通り、 部分積分を楽に解くコツ(下メモ法) を解説しているので、以下の様な人は必見です!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




對數 維基百科 自由的百科全書




自然對數 维基百科 自由的百科全书
問題1 次の広義積分が収束することを示し、値を計算せよ。 (1) ∫ 1 1 1 x p x2 1 dx (2) ∫ 1 1 xtan 1 x p 1 x2 dx (3) ∫ 3 0 1 √ jx(x 2)j dx (4) ∫ 1 0 1 1x3 dx (5) ∫ 1 1 logx xn dx (n = 2;3;) 問題2 広義積分 ∫ 1 0 sinx x dx は収束するが、広義積分 ∫ 1 0 jsinxj x dx は発散する ことを証明せよ。 問題3 a > 0 とし積分 xlogx ∫ x log x d x log x を log x = t とおいて置換積分を行う. x = e t → d x d t = e t → d x = e t d t 与式 = ∫ e t t e t d t = ∫ t e 2 t d t t e 2 t は t と e 2 t の積で, t を微分すると1となる. ⇒ 部分積分をするとよい. f (t) = t , g ′ (t) = e 2 t とした部分積分を行う. · =1 logx=tとおいています 解答にあった解き方広義積分の解き方なのですが このaとはどこから来たのでしょうか 通報する この質問への回答は締め切られました。 質問の本文を隠す A 回答 (2件) ベストアンサー優先;




對數函數積分表 維基百科 自由的百科全書




Logxを0から1まで広義積分するとき 積分の下端をcとおいて計算してからc 0とし Clear
· $$I'(a)=\log (aμ)\log (av)C$$\(I'(\infty)=0\) より \(C=0\) だから$$I'(a)=\log (aμ)\log (av)$$もう一度、両辺を \(a\) で積分します。$$I(a)=(aμ)\log (aμ)(av)\log (aμ)C$$\(I(\infty)=0\) より \(C=0\) だから$$I(a)=(aμ)\log (aμ)(av)\log (aμ)$$\(a=0\) とします。$$I(0)=μ\log μv\log v$$以上より$$\displaystyle\int_0^1 \frac{x^{μ1}x^{v1}}{(\log∫(1/log x) dx = t ^−1 e^t t ^−2 e^t 2 t ^−3 e^t 6t ^−4 e^t Proof Let t = logx => e^t = x => dt= (1/x) dx or dx = e^t dt ∴, ∫(1/log x) dx = ∫e^t dt/t = ∫ t^1 e^t dt Using integration by parts, ∫udv = uv ∫vdu In ∫t^ · 名前 * メール * サイト 次回のコメントで使用するためブラウザーに自分の名前、メールアドレス、サイトを保存する。




Logxの不定積分




請益 Logx的積分 Mobile01
積分電卓 解析積分を用いて所与の変数に対する関数の不定積分(アンチ導出)を計算する。 また、関数のグラフとその積分を描画することもできる。 計算された不定積分は、Cが任意の定数である関数F(x)Cのクラスに属することを覚えておいて下さい。 · 初等関数では表せない積分です。 私もよくわからないのですが,聞きかじったところによると積分対数関数とかいうそうです。 ∫1/xlogx dx なら解けるのに不思議ですね。Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




积分限为0到p 2 被积函数为sinx或者cos的n




Matlab数值微积分与方程求解 码农家园
The following is a list of integrals (antiderivative functions) of trigonometric functionsFor antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functionsFor a complete list of antiderivative functions, see Lists of integralsFor the special antiderivatives involving trigonometric functions, see Trigonometric integral · ∫log (x+1)/x dx これも不思議なのですけど、 ∫ logx x dx はできる 積分 なのに、 ∫ log (x 1) x dx はできない 積分 になります。極限計算機で関数の極限を計算します。片側、両側の極限もサポートされています。極限が計算されるポイントは、たとえばπ/ 4 のような数字または単純な式で指定することができます。極限の計算は正の無限大( inf)、負の無限大( minf
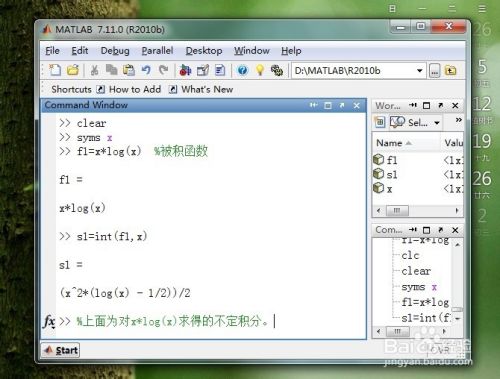



如何用matlab求各种不定积分 百度经验




微積分第六次作業
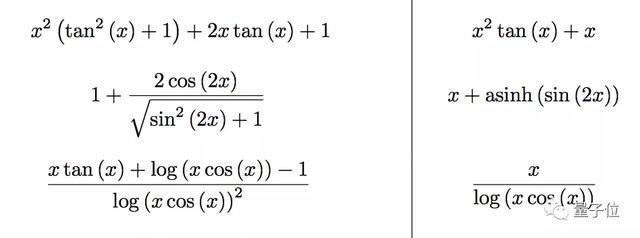



Ai拿下高数一血 求解微分方程 不定积分只需1秒 成绩远超matlab 知乎
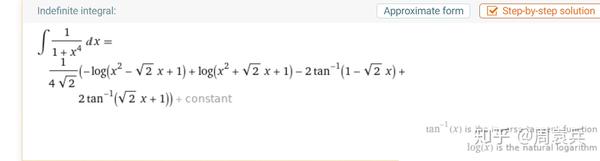



一类关于积分的总结 一 知乎




3 4 5 Function Edit 4callbackh Object Eventdata




高等数学微积分 北大版 Pages 1 50 Flip Pdf Download Fliphtml5



What Is The Integral Of 1 X Logx Quora




Integration Of E X Logx 1 X Dx Youtube



Ap考试微积分公式 二 Ap微积分 一诺留学




Matlab学习与使用 求不定积分 Int 百度经验




Integrate Wolfram 语言参考资料




𝖘𝕲𝖞𝖆 調査票準備 Pa Twitter 友人に 見て数十秒で出来る と言われた不定積分を地道に計算しようとしたところ 0 1 の証明が出来ました どこがマズイんだ




Integrate Logx X




Ap微积分公式大全 翰林国际教育



1




高等数学积分公式大全 It610 Com




Use Mathematica Function To Improve Programmer Sought



高等数学微积分公式全集 沃文网wodocx Com




Mathematica入门习题 25 符号微分与积分 文艺数学君




写真の問題で1 1 Yの積分と1 1 Xの積分がlog 1 Y Log 1 X になる理由 数学 教えて Goo



庆祝运动论网站成立一周年发表文章 微积分的代数根源及其代数化研究 二 数学部分 运动论网站



干货 送你一套数学微积分常用公式大全




Sym Py Edu




What Is The Integration Of 1 Log X Quora



3



如何用matlab求上限积分函数 Matlab基础 Matlab之家




高中数学 导数 与 简单积分 综合复习资料 网络




Ppt Matlab 入门教程powerpoint Presentation Free Download Id




Mathematica练习程序 第三章微积分 Dsp Tian 博客园




正弦函数的积分怎么求 Sin4次方的不定积分怎么求 三人行教育网 Www 3rxing Org



3
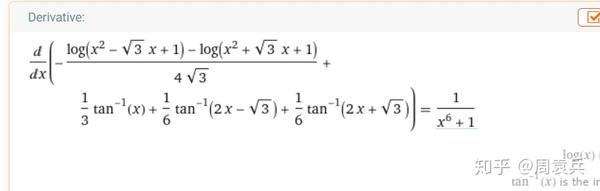



一类关于积分的总结 一 知乎



Ap微积分考前必背公式 高频考点大集合 冲刺5分这些重点你必须掌握 三立国际教育集团sat培训sat考试出国留学



这个对数积分如何计算 知乎



What Is The Integration Of 1 Log X Quora



3




高等数学期末总复习day7 基本不定积分 凑积分 第二类换元法 码农家园




05 第五章用matlab计算积分




05 第五章用matlab计算积分




Integrating Log X Learnmathsfree Youtube



年广州成考专升本数学模拟试题 广州成人高考网




怎样利用matlab求定积分和不定积分 百度经验




自然對數 维基百科 自由的百科全书



如何用matlab求各种不定积分 Matlab基础 Matlab之家
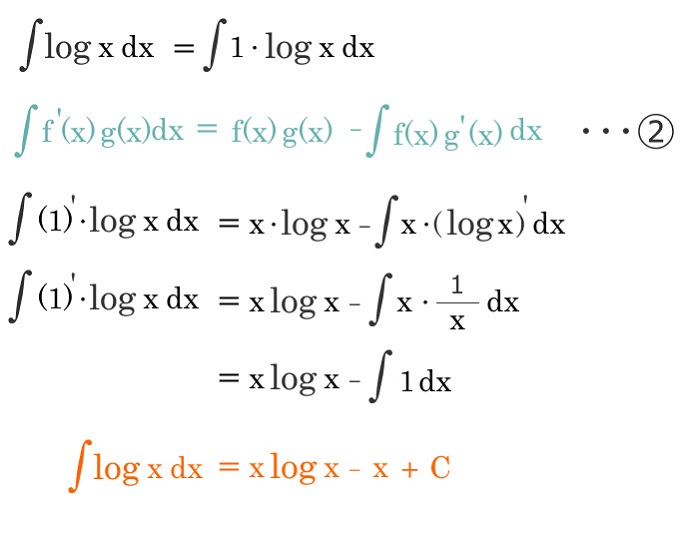



部分積分 優技録




Indefinite Integral Of 1 X Antiderivative Of 1 X Video Khan Academy




Nintegrate 积分策略 Wolfram 语言参考资料




Ap微积分公式表




基本函數的微分和積分公式匯總 每日頭條




筆記 高數筆記 碼上快樂



0から1で Logx X Dxの広義積分の解き方をなるべく詳しく教えてく Yahoo 知恵袋




請益 Logx的積分 Mobile01
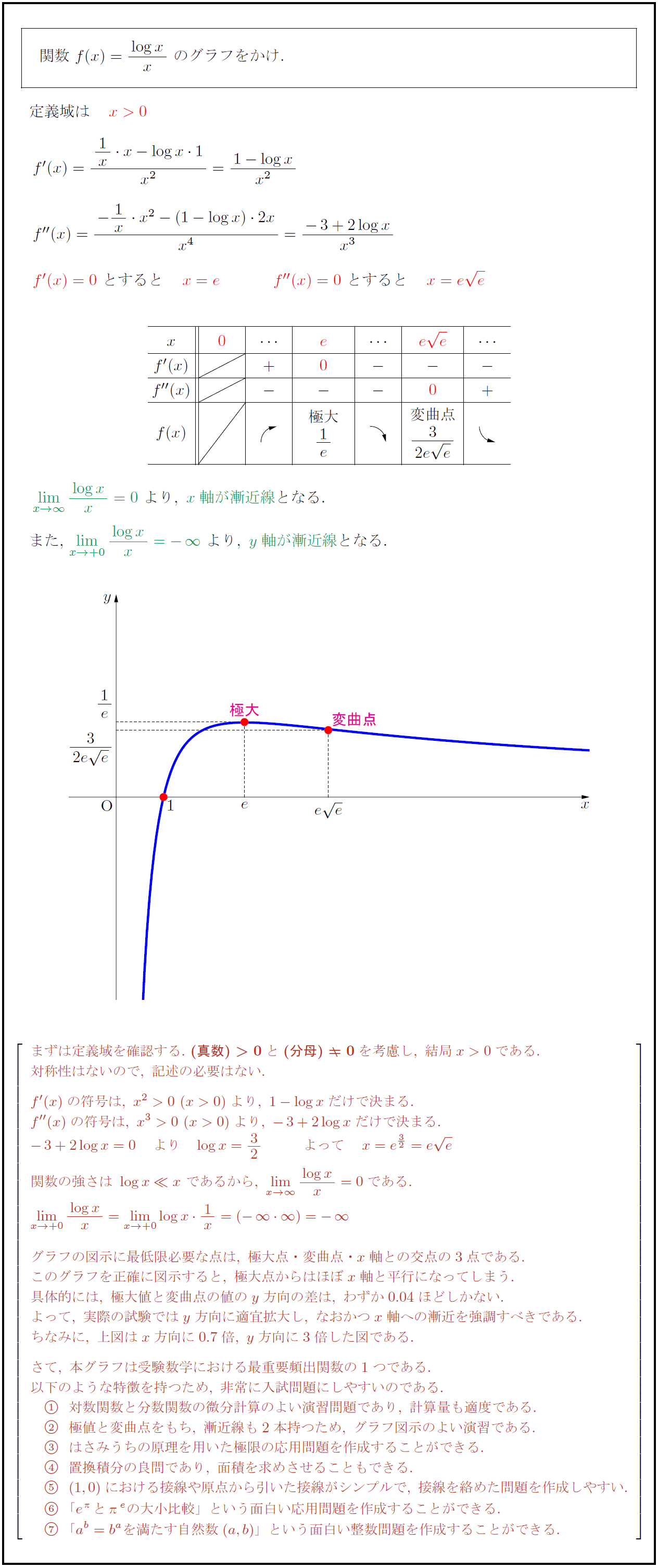



高校数学 対数関数 Y Logx X のグラフ 受験の月




Integral Of Ln X 1 Substitution By Parts Youtube
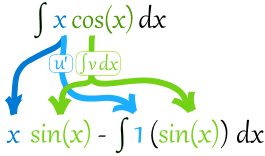



分部积分法



Logxの不定積分について なぜlog X 1 の積分は X 1 Lo Yahoo 知恵袋




定積分の問題 1 E Logx 2 Dx という問題です 答え Okwave




Matlab学习笔记 数值积分 U的博客 Csdn博客 数值积分matlab



这个对数积分如何计算 知乎



Ap考试微积分公式 一 Ap微积分 一诺留学



1 X 1 Logx この積分ができません どなたか教え Yahoo 知恵袋




Ppt 高等数学powerpoint Presentation Free Download Id




Epub Type Visual Novel Gives Us Happy Math A Prototype Of Edutainment Software On Math Semantic Scholar




高中数学 导数 简单积分 最详细的综合复习资料 练一练



高等数学微积分公式 Doc 360文库




自然對數 维基百科 自由的百科全书




数学实验一元微积分基础实验1 函数与极限专题实验1 极限的应用基础实验2 微分及其应用专题实验2 选址问题 Ppt Download




Log X 2 Dxの積分の仕方がわかりません 誰か教えてください Clear




带数学公式的矢量背景向量例证 插画包括有等式 功能 配方 微积分 教育 科学 安纳托利亚




Y Logx Dy Dx
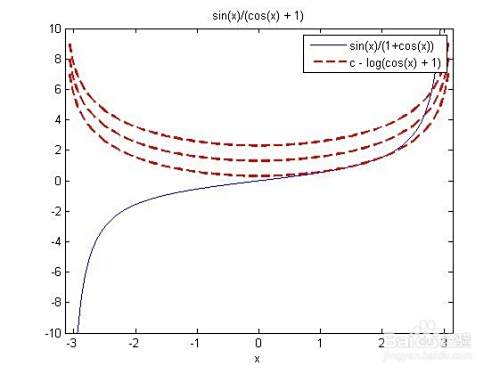



Matlab学习与使用 求不定积分 Int 百度经验



Logxの積分はなんですか 微分なら1 Xですよね Logx Yahoo 知恵袋



Log X 1 の積分の答えってどうなりますか X 1 L Yahoo 知恵袋



1 X Logx の積分計算のやり方を教えてください Lo Yahoo 知恵袋




怎么快速求出被积函数的原函数 定积分中的被积函数是对数函数 怎么求它的原函数 三人行教育网 Www 3rxing Org




Log Xの積分 理系的な戯れ




自然底數e 的定義 上 昌小澤的秘密基地 痞客邦




What Is The Integration Of 1 Log X Quora




数 不定積分 対数関数 Logx Dx オンライン無料塾 ターンナップ Youtube




求不定积分dx X 3x2 4x 1 1 2 雨露学习互助



Ap微积分知识点总结 都涉及哪些内容 A加未来国际教育机构




Matlab计算函数的极限 求导 积分 百度经验
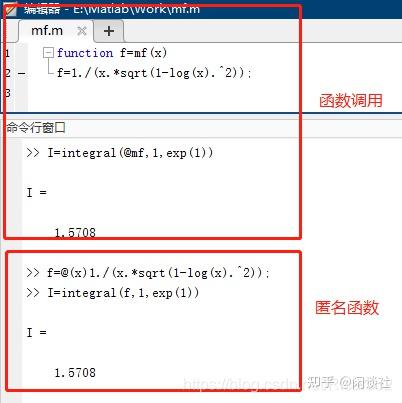



专题六数值微积分与方程求解 知乎




Knowledge Teaching 從雲端數學了解log X 的積分代表式 Understanding Log X Integral Representation From Cloud Math


コメント
コメントを投稿